Background and Theory
This is a pedagogical introduction to crystallography and basic group theory. For information about how PyXtal works specifically, see the Algorithm <Algorithm.html>`_ page.
Crystals and Structures
When studying solids, it is often useful to describe a material’s structure at the atomic level. From this description one can (in theory) determine the material’s physical properties, including mechanical strength, electrical and thermal conductivity, melting point, etc. Due to the near-infinite number of possible materials and atomic geometries, it is necessary to have a consistent mathematical framework. This is described by crystallography.
For an atomic structure, we could describe the geometry by specifying the type and position of every atom. This works alright for molecules, and is in fact how computers typically encode molecules. But for an ideal crystal, which is infinitely large, it is impossible to describe where each individual atom lies. Fortunately, because crystals are symmetrical, we can specify one part of the crystal, and then use the symmetry operations to generate the rest of the crystal. This creates a perfectly symmetrical structure which is infinitely large in size. Such objects do not exist in nature, but they are nevertheless useful for understanding small parts of real, imperfect crystals. So, we call this infinite and symmetrical object an ideal crystal.
Most inorganic materials are formed by many small (nearly) ideal crystals called grains. These grains may have different shapes, sizes, and orientations, but each grain has the same crystal structure at the inter-atomic scale. If we can determine this crystal structure, it becomes possible to predict the way that the grains form and interact with each other. From this, we can go on to predict properties at larger and larger scales, and determine how useful a material will behave in different physical situations. Therefore, determining a material’s small-scale crystal structure is absolutely essential for modern materials science and engineering.
At different pressures and temperatures, a material may go through a solid phase transition, and take on a different crystal structure. So, one job of crystallographers is to determine how a system will change under different conditions. Often, new structures will form at high pressure, and sometimes these structures have vastly superior properties (think diamond .v.s graphite). Thus, high pressure physics forms an active branch of physics and chemistry, and is a potential avenue for finding high temperature superconductors.
Periodicity, Lattices, and Unit Cells
Formally, an ideal crystal is an atomic structure that is periodic in three dimensions. This means that when we translate the structure by a certain amount (in any one of 3 directions unique to the crystal), the crystal will look the same. This can be pictured in a few simple steps:
Define a small parallelepiped-shaped box.
Put atoms into the box (You can put as few or as many atoms as you like.
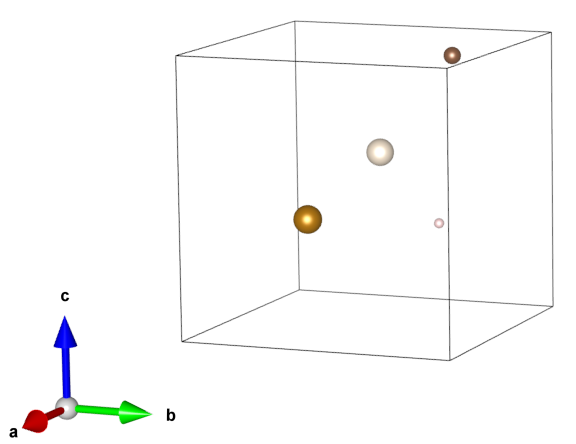
Make a copy of the box and place it adjacent to the original box.
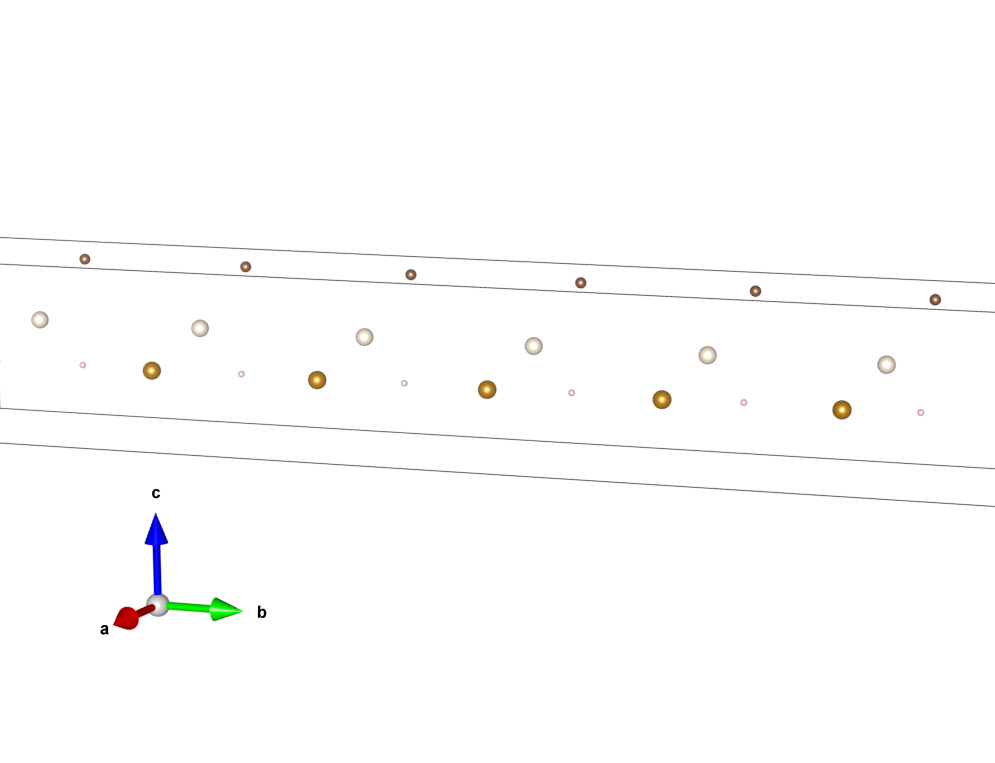
4. Make a copy of the copy, and place that adjacent to the previous one, but along a different axis.
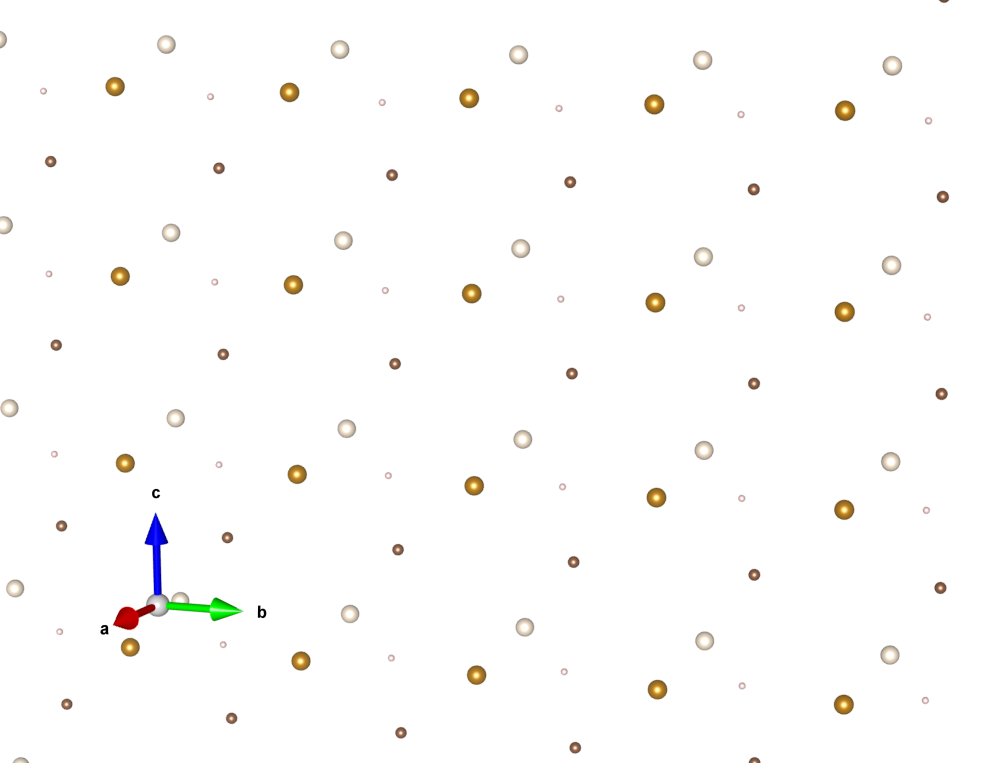
Repeat step 4 until you have filled all of space.

We say that the resulting object has translational symmetry, or that it is periodic. We can be more specific by defining the vectors of translational symmetry. For a given crystal, there are 3 such linearly independent vectors. These 3 vectors, placed into a matrix, define what is called the unit cell. Alternatively, we can define the unit cell using the lengths of each side of the box (usually called a, b, c), along with the angles between them (usually called \(alpha, beta, gamma\)). These 6 values are called the cell parameters. The unit cell is any parallepiped-shaped part of the crystal which can be used to generate the rest of the crystal through translations alone. Any unit cell which has the smallest possible volume is called a primitive cell.
Note: a given crystal can have multiple ways to define a primitive cell, and there is not always a clearly preferred choice. Consider a 2-dimensional square lattice. You could just as well define the lattice using parallelograms which run along the diagonal lines:
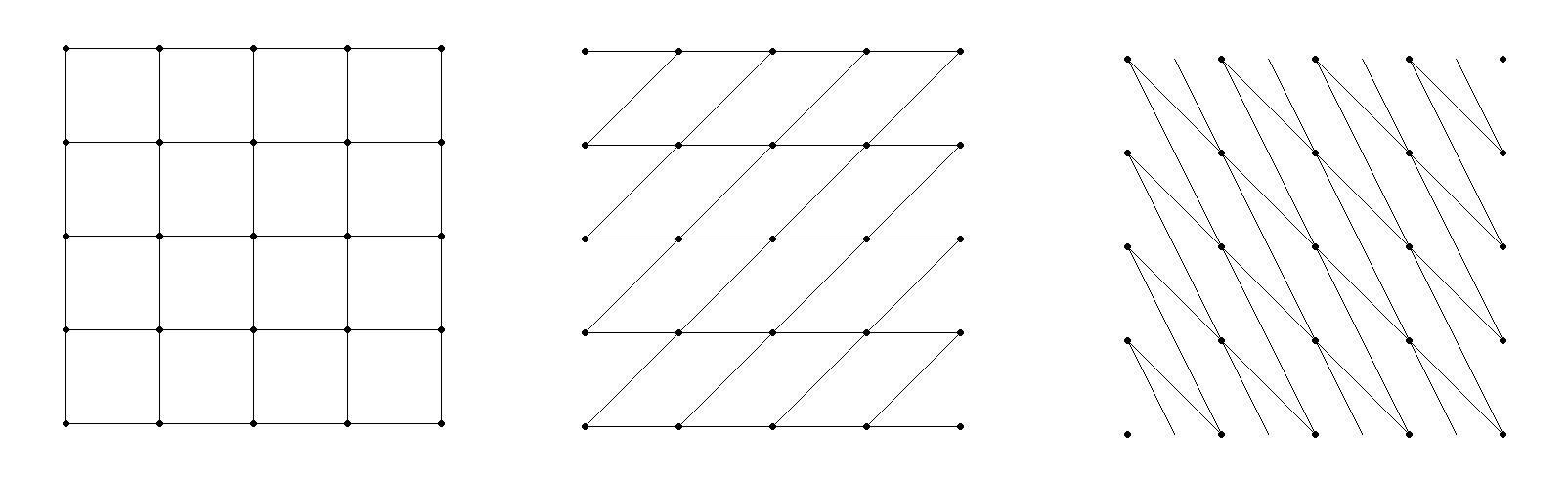
To avoid this confusion, there is a set of standards (defined in the International Tables of Crystallography) which is typically used. A cell based on these standards is called the conventional cell. In many cases, the conventional cell is not actually a primitive cell. Instead, the conventional cell may have extra atoms which exist in specific locations within the cell. So the cell type is determined both by the cell parameters, and by any additional atomic sites within the cell.
Different cell parameters lead to different rotational symmetries of the unit
cell (we will discuss this more below). Based on these symmetries, unit cells
can be divided into seven different crystal classes. Each crystal class has
a different range of allowable cell parameters; triclinic is the general class,
requiring no symmetry. Combining these restrictions with possible extra lattice
positions, we get 14 possible types of lattices, called the Bravais lattices.
We list these here:

Triclinic |
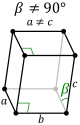
P-monoclinic |

C-monoclinic |
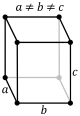
P-orthorhombic |
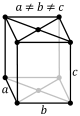
C-orthorhombic |
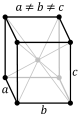
B-orthorhombic |
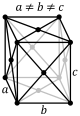
F-orthorhombic |
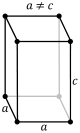
P-tetragonal |
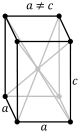
B-tetragonal |
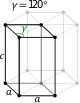
Hexagonal |
Rhombohedral |
R-cubic |
Body-centered cubic |

|
Much like squares can be considered a special case of rectangles, all unit cells
can be thought of as special cases of triclinic cells. Cubic cells are a subset
of tetragonal cells, tetragonal cells are a subset of orthorhombic cells, and so
on. The hexagonal and trigonal lattices are somewhat special cases. They can be
generated using either trigonal/hexagonal prisms, or using the standard
parallelepiped shape. For consistency, the parallelepiped is always used. Note
that despite using a parallelepiped, this is still called a hexagonal cell choice.
Some lattices can be generated using a rhombohedral unit cell. Such space groups
begin with an R, and always have trigonal symmetry. For these cases, we
again use the hexagonal cell.
Whenever possible, PyXtal uses the same choices of unit cell as the Bilbao Crystallographic Server, which in turn uses the standard conventional cell. For a complete list of the cell choices used by PyXtal, see the Group Settings page.
Typically, to describe coordinates within a crystal, we use what are called fractional coordinates. Fractional coordinates use the lattice vectors as the basis, as opposed to absolute coordinates, which use Euclidean space as the basis. This makes it easier to describe two similar structures that differ only in their lattice values. Unless otherwise specified, any listed coordinates are fractional coordinates.
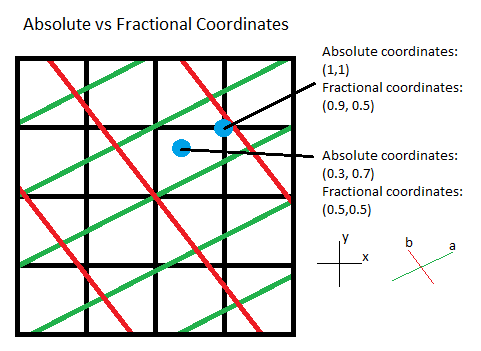
It is important to note that when periodicity is present, multiple coordinates
can actually correspond to the same point, at least in notation. It is common
practice to convert all coordintaes to lie within the range [0, 1) for periodic
axes. So, for example, if we have a point at (1.4,-0.3,0.6), it will usually
be written as (0.4,0.7,0.6). This is because it is assumed that each unit
cell is the same. In other words, an atom located at (1.4,-0.3,0.6) implies
that another atom is located at (0.4,0.7,0.6). So, it is more convenient to
only consider the unit cell which lies between (0,0,0) and (1,1,1).
Symmetry Operations
Translations are just one kind of transformation operation. More generally, we can perform any 3-dimensional transformation which preserves the lengths and angles between atoms. This means we can also apply rotations, reflections, and inversions, as well as any combination of these. Note that successive operations do not generally commute. That is, the order of operations determines the final outcome.
A symmetry operation is any transformation which leaves the original structure unchanged. In other words, if the structure looks the same before and after a transformation, then that transformation is a symmetry operation of the object. This includes the identity operation (doing nothing to the object), which means that every object has at least a trivial symmetry.
We can artificially split a transformation into two parts: the rotational and
inversional part (given by a 3x3 matrix), and the translational part (given by a
3D vector, specifically a 3x1 column matrix). Often, we denote this as a
matrix-column pair (P,p) or (P|p), where the capital letter P represents
the rotation matrix, and the lowercase letter p represents the translation vector.
We can define the 3x3 rotation matrix by using 3 orthogonal unit vectors as the columns. The resulting matrix is orthogonal, meaning the determinant is either +1 or -1. If only a rotation is applied, then the determinant is +1, and if an inversion is applied, the determinant is -1. If an object has no symmetry operations with determinant -1, it is said to be chiral. In this case, the object’s mirror image is different from the original, and cannot be rotated to match its twin. This is especially important for molecules with biochemical applications, since the mirror molecule may have a different effect.
Now, we can define how one operation is applied to another. We consider two
operations: (P,p) and (Q,q). If we first apply (P,p), followed by
(Q,q), then we get a new operation, which we will call (R,r): (Q,q)(P,p) = (R,r).
Note that we apply operations from the left. Then, the relationships are:
R = Q*P
r = Q*p + q
where * denotes standard matrix multiplication. From this definition, we see that
the rotation is always applied first, followed by the translation. This rule
applies for multiple operations as well; with 3 operations (R,r)(Q,q)(P,p),
we first apply (P,p), then (Q,q), then (R,r).
Alternatively, the matrix-column pair can be combined into a single 4x4 matrix. We simply place the vector to the right of the rotation matrix, place 0’s on the bottom row, and place a 1 in the lower right-hand corner:
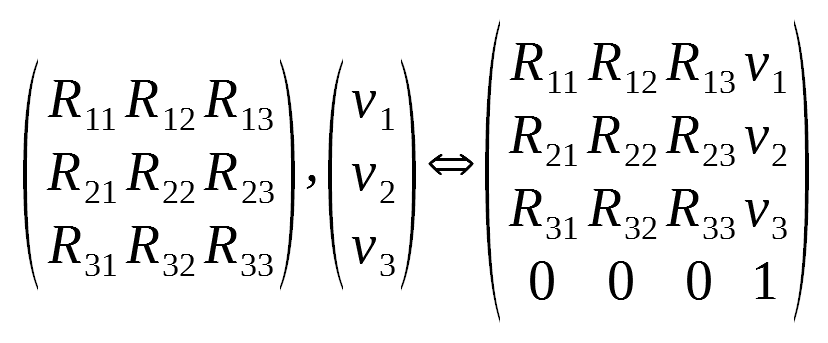
This matrix is called an affine transformation matrix. With it, we can apply
operations using a single matrix multiplication operation. Although this may
seem like just a mathematical trick, the affine matrix notation highlights the
group structure of the transformations, as it allows translations and rotations
to be placed on equal footing. Furthermore, we can use the additional dimension
to represent time: the ‘1’ value can be thought of as a single step forward in
time, and thus we can define both rotational and translational reference frames
(and equivalently, torques and forces) with a single 4x4 matrix. Objects which
are (periodically) symmetric in time are called time crystals. Such objects have
only recently been synthesized in the lab, and there is likely more research to
be done. However, for most applications in crystallography, time is not a factor,
and we consider only spatial symmetries.
Sometimes crystallographers express an affine transformation as a list of letters
and numbers, separated by commas (for example, x,y,z). In this notation, the
first, second, and third positions denote what happens to the unit x, y, and z
axes, respectively. So if we want to perform an inversion, we replace each axis
with its opposite. Then, x,y,z becomes -x,-y,-z. So, you can use
-x,-y,-z to represent an inversion. Similarly, y,-x,z would represent a
90 degree rotation about the z axis (using the right hand rule). You can also
map to a linear combination of axes, or add a constant value. So, you might see
something like x-y,x,z+1/2. Here, we just follow the same procedure: x, which
is the vector (1,0,0) is mapped onto x-y, which is the vector (1,-1,0).
y (0,1,0) is mapped onto x (1,0,0), and z (0,0,1) is mapped onto
z+1/2 (0,0,1), or in the 4x4 notation, (0,0,1,.5). To express the
addition of a constant (in this case 1/2 for the z-axis), the right-hand side of
the 4x4 matrix is used. So, we would write x-y,x,z+1/2 as:
![[[1,-1,0,0],[1,0,0,0],[0,0,1,0.5],[0,0,0,1]]](_images/affine_matrix.png)
Note that the mapped vectors are written as rows, NOT columns. So, x-y is
written on the first row as (1,-1,0,0). Again, the bottom row is always
(0,0,0,1), so that matrix multiplication is preserved.
Groups
Symmetry operations have several nice properties, and this allows certain sets of them to be classified as a mathematical object called a group. There are several simple and intuitive examples of groups, which we will discuss below. Formally, a group G is a set of mathematical objects (called elements) with 4 properties:
1) There is a binary operation which maps any two elements in the set onto a
third element which is also in the set: A*B = C. The operation must be
defined for every possible pair on the set, and must map onto an element which
is inside of the set.
2) There must be exactly one identity element I which maps every element of
the set onto itself: A*I = I*A = A for every A in G.
3) Every element A must have an inverse A^-1, such that multiplication
by the inverse gives the identity: A*A^-1 = A^-1*A = I.
The operation * must be associative. That is,
(A*B)*C = A*(B*C).
Note that commutativity is not a requirement for groups, but associativity is. Anticommutativity has important implications for describing rotations and angular momentum in 3 dimensions, which are beyond the scope of this study.
One of the simplest examples of a group is the additive group of real integers
(Z,+). Here, the set is that of the integers (-1, 0, 1, ...), and the
operation is addition. Here, the inverse of a number is just its negative.
For example, the inverse of -2 is 2. One can easily verify that the 4 properties
listed above hold true for this group. Similarly, we can consider the additive
group of real numbers (R,+), or the additive group of complex numbers (C,+).
However, if we replace addition with multiplication, then we no longer have a group, because the element 0 does not have a multiplicitive inverse: any number multiplied by 0 is 0, but any number divided by 0 is undefined. We can fix this by considering the multiplicative group of all numbers except for 0. Or, equivalently, we can consider the multiplicitave group exp(x), where x is any complex number. Then, the inverse is defined as exp(-x), and the identity element is exp(0) = 1.
Interestingly, the real numbers are a subset of the complex numbers, and yet both the complex numbers and the real numbers form groups in their own right. In this case, we call the real numbers a subgroup of the complex numbers. Likewise, we call the complex numbers a supergroup of the real numbers. More specifically, we say that the real numbers are a proper subgroup of the complex numbers, because there are fewer real numbers than complex numbers. Likewise, the complex numbers form a proper supergroup of the real numbers. So, a group is always both a subgroup and a supergroup of itself, but is never a proper subgroup or proper supergroup of itself.
These are so far all examples of infinite groups, since there are infinitely
many points on the number line. However, there also exist finite groups. For
example, consider the permutation group of 3 objects (we’ll call them a,
b, and c). Our group elements are:
1: (a,b,c)
2: (a,c,b)
3: (b,a,c)
4: (b,c,a)
5: (c,a,b)
6: (c,b,a)
As you can see, there are only 6 elements in this group. Element (1) is the
identity, as it represents keeping a, b, and c in their original
order. Element (2) represents swapping b and c, element (3) represents
swapping a and b, and so on.
In general, we call the number of elements in a group the order of that group. In the example above, the order is 6. If there are an infinite number of elements in a group (for example, the additive group of real numbers), we say the group has infinite order. A group of order 1 is called a trivial group, because it has only one element, and this must be the identity element. Furthermore, because every group has an identity element, every group also contains a trivial group as a subgroup.
Sometimes, it is inconvenient to list every member of a group. Instead, it is often possible to list only a few elements, which can be used to determine, or generate the other elements. These chosen elements are called generators. For example, consider elements (2) and (3) in the permutation group shown above. We can define the remaining elements (1, 4, 5, and 6) starting with only (2) and (3) (with operations acting from the left):
2 * 2 = 1 : (a,c,b) * (a,c,b) = (a,b,c)
2 * 3 = 4 : (a,c,b) * (b,a,c) = (b,c,a)
3 * 4 = 6 : (b,a,c) * (b,c,a) = (c,b,a)
6 * 2 = 5 : (c,b,a) * (a,c,b) = (c,a,b)
Thus, we say that (2) and (3) are generators of the group. Typically, there is not a single best choice of generators for a group. We could just as easily have chosen (2) and (6), or (4) and (3), or some other subset as our generators.
Symmetry Groups
One can verify that the four properties of groups listed above also hold for our 4x4 transformation matrices. Thus the set of all 3D transformations (with 4x4 matrix multiplication as our operation) forms a group. Because of this, the tools of group theory become available.
When we want to define the symmetry of an object, we specify the object’s symmetry group. A symmetry group is just the set of all of the object’s symmetry operations (described above). It turns out, the set of all symmetry operations for an object always forms a group. The group properties (2-4) hold because we are using 4x4 transformation matrices, which are already a group. Property (1) holds because a symmetry group is always a closed set. This is because performing any symmetry operations always brings us back to our original state, and therefore combining multiple symmetry operations also brings us back to the original state. Thus, combinations of symmetry operations are themselves symmetry operations, and are therefore elements of the object’s symmetry group.
The simplest 3D symmetry group is the trivial group (called “1”). This group has only the identity transformation I, which means that it corresponds to a completely asymmetrical object. For such an object, there is no transformation (besides the identity) which brings the object back to its original state. Most molecules have at least some rotational symmetry, and crystals always have at least translational symmetry, so we will not encounter this group very often.
On the other hand, we can consider empty 3D space, which is perfectly symmetrical (note: this does not apply to actual empty space, which contain gravitational and quantum fields). The symmetry group of empty space includes not only rotations and translations, but also scaling and shearing, since nothing will always be mapped back onto nothing.
Note that only empty space, or other idealized objects (including some fractals) can have scaling symmetry. For atomic structures, we will never encounter this. However, shear symmetry is possible for lattices. As an example, consider the different choices for the primitive cell shown in the section above. These different primitive cells can be mapped onto each other using shear transformations. It is important to note that in general only simple lattices have this shearing symmetry; if there are atoms inside of the lattice, they may not map onto other atoms in the crystal.
We can also define symmetry groups for objects of arbitrary dimension. A simple example is the equilateral triangle, which has a 3-fold rotational symmetry, as well as 3 reflectional symmetries. A slightly more complex example is the regular hexagon, which has all of the symmetries of the triangle, but also 6-fold and 2-fold rotational symmetry, and additional reflectional symmetries. Combining rotation and reflection, the hexagon also has the inversion symmetry:
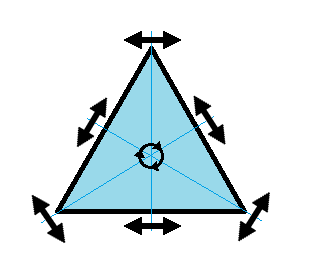
triangular symmetry |
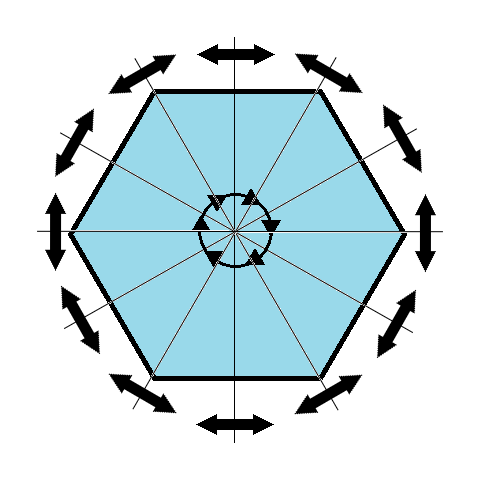
hexagonal symmetry |
It takes practice to develop an intuition for finding symmetries, but the results can be very rewarding. Often, a symmetry can be utilized to lessen the work needed to solve a problem, sometimes even reducing the problem to a trivial identity. This is a core concept in mathematics and physics, and deserves reflection.
Point Groups
In order for an object to be translationally symmetric, it must be periodic along one or more axes. This means that most objects (excluding crystals and certain idealized chain molecules) can only have rotational/inversional symmetry. A 3D symmetry group without translational symmetry is called a point group. This is because the transformations leave at least one point of space unmoved. This includes rotations, reflections, inversions, and combinations of the three. Note that we can either use rotations and reflections, or rotations and inversions, to generate the remaining point transformations. In PyXtal and the documentation, we use rotations and inversions as the basic transformations, meaning reflections are treated as rotoinversions.
A point group can contain rotations, reflections, and possibly inversion. There are several conventions for naming point groups, but PyXtal uses the Schoenflies notation. Here, point groups have one or two letters to describe the type(s) of transformations present, and a number to describe the order. For detailed information, see the Wikipedia page. Below are a few examples of point groups found in crystallography and chemistry.
\(H_2O\): point group C2v (2-fold rotation axis, and two mirror planes) [2]
Hypothetical Pmmm crystal: point group mmm (3 mirror planes)
Buckminsterfullerene: point group Ih (Full icosahedral symmetry) [3]
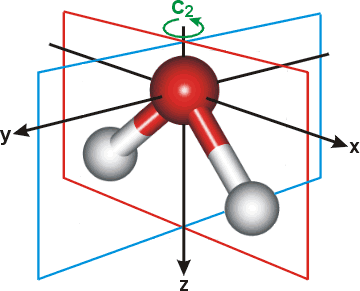
\(H_2O\) molecule ( |
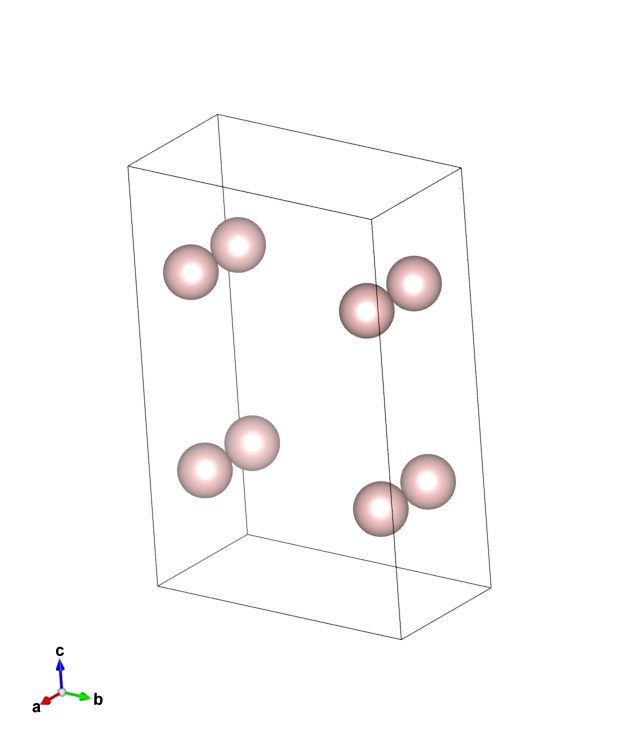
Hypothetical crystal ( |

Buckminsterfullerene ( |
Space Groups
For crystals, we need to describe both the translational (lattice) and rotational (point group) symmetry. A 3D symmetry group containing both of these is called a space group, and is one of the main tools used by crystallographers. We can separate a space group into its point group and its lattice group. Thus, space groups can be neatly divided into the seven different crystal classes. Mathematically, the two different types of symmetry are connected; thus, certain kinds of translational symmetry (lattice types) can only have certain kinds of rotational symmetry (point groups). This is apparent from the names of the space groups; certain symbols are only found in certain lattice systems. A list of space groups and their symmetries is provided by the Bilbao utility WYCKPOS. Note that for space groups, we use the Hermann-Mauguin (H-M) notation. This means a space group can be specified by a number between 1 and 230. However, a space group symbol should always be provided, as the numbers are not used as commonly. The numbers are more useful for computer applications like PyXtal or Pymatgen, or in conjunction with references like the Bilbao server or the International Tables.
Technically speaking, two crystals with the same lattice type and point group, but with different cell parameters, have different space groups. The space group is the set of all symmetry operations, and in this case the translational symmetry operations would be different. But typically when someone says space group, they actually mean the set of all space groups with the same lattice type and point group. In this sense, we say that there are 230 different space groups. This is the meaning of space group which we will use from now on, unless otherwise specified. This is useful, since we don’t need to define a new space group every time we shrink or stretch a crystal by some small amount.
Not every rotational symmetry is compatible with a 3D lattice. Specifically, only rotations of order 2, 3, 4, or 6 are found in real crystals (Note: pseudo-crystals may have different local symmetries, but lack long-range periodicity). As a result, only 32 point groups are found as subgroups of space groups. These are called the crystallographic point groups. So, by choosing such a point group, along with a compatible lattice, we define a space group. By compatible lattice, we mean any lattice which maps onto itself under the symmetry operations of the chosen point group. Because of this compatibility condition, the presence of a particular symmetry can tell you what kind of lattice is present. For example, a 6-fold rotation always belongs to a hexagonal lattice. A 3-fold rotation about one of the primary axes belongs to a trigonal axis, whereas a 3-fold rotation about the diagonal belongs to a cubic lattice. In this way, the lattice type can be determined from the Hermann-Mauguin symbol.
In reality, a crystal is often distorted slightly from its ideal symmetrical
state. As a result, two researchers may label the same crystal with different
space groups. This phenomenon is called pseudosymmetry; it is when a crystal is
close to possessing a certain space group, but is only slightly off. This is a
real problem for computational crystallography, since numerical accuracy makes
determining symmetry an imprecise business. For example, if an atom is located
at (0,1/3,0), it will be encoded as something like (0,.33333,0) due to
rounding. As a result, it will be slightly off from the expected location, and
the computer may not recognize the 3-fold symmetry. So, whenever you work with
crystal symmetry, it is a good idea to allow some numerical tolerance
(roughly somewhere between .001 and .03 Angstroms), so as to correctly
assess the symmetry. On the flip side, if a provided crystal is labeled as
having P1 symmetry (which means no rotational symmetry was found), it is likely
that some symmetry is actually present, but was not found due to numerical issues.
Wyckoff Positions
Because symmetry operations can be thought of as making copies of parts of an object, we can usually only describe part of a structure, and let symmetry generate the rest. This small part of the structure used to generate the rest is called the asymmetric unit. However, not all points in the asymmetric unit are generated the same. If an atom lies within certain regions - planes, lines, or points - then the atom may not be “copied” as many times as other atoms within the asymmetric unit. A familiar example is in the creation of a paper snowflake. We start with a hexagon, then fold it into a single triangle 6 sheets thick. Then, if we cut out a mark somewhere in the middle of the triangle, the mark is copied 6-fold. However, if we instead cut out a mark alonng the triangle’s edge, or at the tip, the marks will only have 3 or 1 copies:
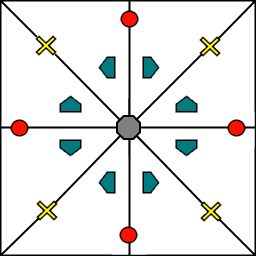
These different regions are called Wyckoff positions, and the number of copies is called the multiplicity of the Wyckoff position. So, if an atom lies in a Wyckoff position with multiplicity greater than 1, then that Wyckoff position actually corresponds to multiple atoms. However, thanks to symmetry, we can refer to all of the copies (for that particular atom) as a single Wyckoff position. This makes describing a crystal much easier, since we no longer need to specify the exact location of most of the atoms. Instead, we need only list the space group, the lattice, and the location and type of one atom from each Wyckoff position. This is exactly how the cif file format encodes crystal data (more info below). Just keep in mind that in this format, a single atomic entry may correspond to multiple atoms in the unit cell.
The largest Wyckoff position, which makes a copy for every symmetry operation, is called the general Wyckoff position, or just the general position. In the snowflake example, this was the large inner region of the triangle. In general, the general position will consist of every location which does not lie along some special symmetry axis, plane, or point. For this reason, the other Wyckoff positions are called the special Wyckoff positions.
The number and type of Wyckoff positions are different for every space group; a
list of them can be found using the
Bilbao utility WYCKPOS. In the
utility, Wyckoff positions are described using the x,y,z notation, where
each operation shows how the original (x,y,z) point is transformed/copied.
In other words, if we choose a single set of coordinates, then plugging these
coordinates into the Wyckoff position will generate the remaining coordinates.
As an example, consider the general position of space group P222 (#16),
which consists of the points (x,y,z), (-x,-y,z), (-x,y,-z), and (x,-y,-z).
If we choose a random point, say (0.321,0.457,0.892), we can determine the
remaining points:
(x,y,z)->(0.321,0.457,0.892)
(-x,-y,z)->(0.679,0.543,0.892)
(-x,y,-z)->(0.679,0.457,0.108)
(x,-y,-z)->(0.321,0.543,0.108)
Here a negative value is equal to 1 minus that value (-0.321 = 1 - 0.321 = 0.679).
To denote Wyckoff positions, a combination of number and letter is used. The
number gives the multiplicity of the Wyckoff position, while the letter
differentiates between positions with the same multiplicity. The letter ‘a’ is
always given to the smallest Wyckoff position (usually located at the origin or
z axis), and the letter increases for positions with higher multiplicity. So,
for example, the space group I4mm (#107) has 5 different Wyckoff positions:
2a, 4b, 8c, 8d, and 16e. Here, 16e is the general
position, since it has the largest multiplicity and last letter alphabetically.
Note that for space groups with non-simple lattices (those which begin with a
letter other than ‘P’), the Wyckoff positions also contain fractional translations.
Take for example the space group I4mm (#107). The Bilbao entry can be found
here.
Each listed Wyckoff position coordinate has a copy which is translated by
(0.5,0.5,0.5). It is inconvenient to list each of these translated copies
for every Wyckoff position, so instead a note is placed at the top. This is why
Wyckoff position 16e has only 8 points listed. In this case, to generate the
full crystal, one could apply the 8 operations listed, then make a copy of the
resulting structure by translating it by the vector (0.5,0.5,0.5). Note that
in space groups beginning with letters other than P, the smallest Wyckoff
position will never have a multiplicity of 1.
In addition to the generating operations, the site symmetry of each Wyckoff position is listed. The site symmetry is just the point group which leaves the Wyckoff position invariant. So, if a Wyckoff position consists of an axis, then the site symmetry might be a rotation about that axis. The general position always has site symmetry 1, since it corresponds to choosing any arbitrary structure or location can be made symmetrical by copying it and applying all of the operations in the space group.
Finally, since crystals are infinitely periodic, a Wyckoff position refers not
only to the atoms inside a unit cell, but every periodic copy of those atoms in
the other unit cells. Thus, the Wyckoff position x,y,z is the same as the
position x+1,y+1,z, and so on. This is usually a minor detail, but it must
be taken into account for certain computational tasks.
Molecular Wyckoff Positions
In most cases, it is assumed that the objects occupying Wyckoff positions will be atoms. Because atoms are spherically symmetrical, they will always possess the site symmetry associated with a given Wyckoff position. However, this is not always the case for molecules, which have their own point group symmetry. Because of this, a given molecule may or may not fit into a given Wyckoff position, depending on its symmetry and orientation.
In order for a molecule to fit within a Wyckoff position, its point group must be a supergroup of the position’s site symmetry. In other words, the molecule must be at least as symmetrical as the region of the Wyckoff position itself (with reference to the operations of the space group as a whole). Furthermore, the molecule must be oriented in such a way that its symmetry axes line up with the symmetry axes of the Wyckoff position. As an example, consider a Wyckoff position with site symmetry 2. This is an axis with 2-fold symmetry. Now consider a water molecule lying on this axis. In order to truly occupy the Wyckoff position, the water molecule’s 2-fold axis must line up with the Wyckoff position’s (See the water molecule image above).
For larger site symmetry groups, it is more complicated to check if a molecule will fit or not. The algorithm used by PyXtal for doing this is detailed in the How PyXtal Works page.
Crystal File Formats
There are two main file formats used for storing crystal structures: cif and POSCAR. Each of these has standard definitions. Here is the cif file definition (given by the International Tables), and here is the POSCAR file definition (given by Vasp).
Cif uses the space group symmetry to compress the data. The core information consists of the space group, the lattice, and the location and type of a single atom from each Wyckoff position. So, for high symmetry space groups, a cif file can be much smaller than a POSCAR file. As with any type of compression, the cif file has the downside that the program using it must be able to work with symmetry operations. Specifically, each Wyckoff position’s generating atom must be copied using the symmetry operations, so that the entire unit cell can be known.
In contrast, a POSCAR file does not provide the symmetry information, but instead specifies the type and location of every atom in the unit cell, including those which are symmetrical copies of each other. This results in a larger file, but one that is easier to read, since no symmetry operations need to be applied. The downside is that if one wishes to know the space group, it must either be calculated, or given by some external source.
Each format has advantages and disadvantages. A computational crystallographer should be familiar with both, and understand the differences. If you provide a POSCAR file for a structure, you should also provide the symmetry group. Likewise, if you provide a cif file, you should be certain that the symmetry information is correct, and that you are using the correct space group setting.